Streu-Experimente mit festem Target - Der Wirkungsquerschnitt (Beispiel)   Welchen Wirkungsquerschnitt hat ein negativ geladenes Streuzentrum für ein anfliegendes Elektron (Stoßparameter b) bei Coulomb-Streuung?     Mit dem Wissen über den Wirkungsquerschnitt können wir diese Frage auch anders formulieren:  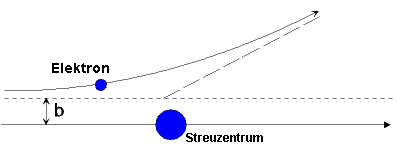  Wie groß ist die Fläche, die das Streuzentrum dem Elektron bietet, so dass es bei Eintritt in diese Fläche eine Wirkung (hier: elektromagnetische Abstoßung) erfährt?    Das für die Abstoßung verantwortliche Coulomb-Potenzial ist radialsymmetrisch, es hängt also nur vom Abstand Elektron-Streuzentrum ab. Die gesuchte Fläche ist folglich eine Kreisfläche in deren Mittelpunkt das Streuzentrum sitzt.     Man kann daher noch einfacher fragen: In welchem Abstand vom Streuzentrum erfährt des Elektron gerade noch eine abstoßende Wirkung?  Man erkennt, dass sich das Problem auf die Frage nach der "Grenze des Wirkungsbereichs" des Coulomb-Potenzials reduziert. Da dieses Potenzial eine unendliche Reichweite besitzt, wird das Elektron immer eine Wirkung erfahren, die zwar mit wachsendem Abstand schnell sehr klein wird, aber immer vorhanden ist. Die Antwort muss folglich lauten: Der Wirkungsquerschnitt ist unendlich groß ( s = ¥ ). Diese Aussage kann man durch Rechnung leicht bestätigen . Es lassen sich aus dem Ergebnis ( s = ¥ ) keine Rückschlüsse auf die Struktur des Targets bzw. das Potenzial ziehen. Man muss daher das Coulomb-Potenzial bei einer bestimmten Größe theoretisch begrenzen, d.h. räumlich auf einen   bestimmten Bereich beschränken. Mit diesem Trick lassen sich dann Aussagen machen.   Eine andere Möglichkeit ist die Betrachtung des differenziellen Wirkungsquerschnitts. Dazu später mehr.  Wie auf dieser und der vorhergehenden Seite beschrieben, lässt sich der Wirkungsquerschnitt als Inhalt einer Streufläche interpretieren.    Der Wirkungsquerschnitt ist damit Maß für die Wahrscheinlichkeit einer Reaktion zwischen Teilchen und Target (aus vielen Streuzentren bestehend). Dazu mehr auf der nächsten Seite.