|
Angeregte
Zustände & Co. -
Resonanzen
|
Wie erwähnt, können nicht nur Atome und Atomkerne angeregte Zustände annehmen, sondern auch Baryonen und Mesonen. Die ersten, die angeregte Atomzustände
gezielt erzeugt und nachgewiesen haben, waren J. Franck
|
und G. Hertz,
die
Elektronen
auf Quecksilberatome
schossen und diese durch die Stöße anregten. Kann man Baryonen, z.B. Protonen auch auf diese Weise anregen?
|
|
 Was passiert, wenn man
hochenergetische
Elektronen (z.B.
E = 4879 MeV
!) auf
Protonen schießt bzw. an Protonen streut?
Was passiert, wenn man
hochenergetische
Elektronen (z.B.
E = 4879 MeV
!) auf
Protonen schießt bzw. an Protonen streut?
|
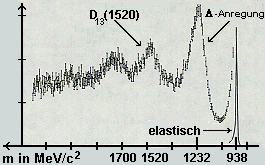
Das Spektrum einer solchen Streuung von Elektronen an Protonen ist rechts abgebildet. Bei der Messung werden Impuls und Energie eines
elastisch oder
unelastisch gestreuten Elektrons registriert und die jeweilige Differenz zu den Werten vor der
Streuung berechnet. Die Differenzen müssen als Impuls- und
Energieübertrag
an das Proton abgegeben worden sein. Der Energieübertrag führt
zu einem "
Massenzuwachs
" des Protons.
In der Abb. rechts ist die
Häufigkeit
dargestellt, mit der man die "neue Masse" findet. Sie wird aus Protonenmasse und dem
Energieübertrag
|
des gestreuten Elektrons errechnet.
Man beachte, dass
die horizontale Achse bei 938
MeV/c
2
beginnt und nach links ansteigend skaliert ist. Man erkennt bei 938 MeV/c
2
,
1232 MeV/c
2
und 1520 MeV/c
2
Maxima
.
 |
|
 Das schmale Maximum bei
938 MeV/c
2
wird durch die
elastische Streuung der Elektronen an Protonen verursacht.
Die Protonenmasse beträgt 938 MeV/c
2
. Die "neue Masse" des Protons ist daher gleich seiner Masse vorher, also
938 MeV/c
2
. Das schmale Maximum ist hier 15-fach verkleinert dargestellt, um die Abbildung
übersichtlich zu gestalten.
Das schmale Maximum bei
938 MeV/c
2
wird durch die
elastische Streuung der Elektronen an Protonen verursacht.
Die Protonenmasse beträgt 938 MeV/c
2
. Die "neue Masse" des Protons ist daher gleich seiner Masse vorher, also
938 MeV/c
2
. Das schmale Maximum ist hier 15-fach verkleinert dargestellt, um die Abbildung
übersichtlich zu gestalten.
 Das zweite und dritte breitere Maximum bei
1232
MeV/c
2
und
1520 MeV/c
2
bedeutet, dass auch besonders häufig Teilchen der Masse 1232 MeV/c
2
und 1520 MeV/c
2
produziert wurden,
die bei
unelastischer
Streuung entstehen.
Das zweite und dritte breitere Maximum bei
1232
MeV/c
2
und
1520 MeV/c
2
bedeutet, dass auch besonders häufig Teilchen der Masse 1232 MeV/c
2
und 1520 MeV/c
2
produziert wurden,
die bei
unelastischer
Streuung entstehen.
 Die
Interpretation dieses Ergebnisses ist, dass die Nukleonen einen
angeregten
Zustand mit den Massen 1232 MeV/c
2
und 1520 MeV/c
2 besitzen, die sogenannte
Delta-Resonanz
D
(1232) (oder Delta-Anregung), und die
D
13
(1520)- Resonanz
.
Die
Interpretation dieses Ergebnisses ist, dass die Nukleonen einen
angeregten
Zustand mit den Massen 1232 MeV/c
2
und 1520 MeV/c
2 besitzen, die sogenannte
Delta-Resonanz
D
(1232) (oder Delta-Anregung), und die
D
13
(1520)- Resonanz
.
Angeregte Zustände
von Protonen und Neutronen (Nukleonen) nennt man
|
aufgrund des "Resonanz-Berges",
durch den sie sich in einer entsprechenden Messauswertung verraten,
Nukleonenresonanzen
. Analog dazu spricht man, wenn man angeregte Zustände von Baryonen
und Mesonen meint, von
Baryonen-
und
Mesonenresonanzen oder ganz allgemein
nur von
Resonanzen. (siehe dazu auch
![zum Literaturverzeichnis; [POV 1994, S. 79]](../button_gifs/booksm.gif) )
)
|
|
Anmerkungen:
Im Prinzip könnte
man den angeregten Zustand eines Quecksilberatoms auch "
Atom-Resonanz
"
nennen. Allerdings wird dieser angeregte Zustand
nicht
wie bei den Nukleonenresonanzen
als eigenes Teilchen
interpretiert, sondern eben
nur als angeregter
Zustand
des Quecksilberatoms bezeichnet. Anderseits könnte
man bei der
D
(1232)-Resonanz auch nur von einem angeregten Zustands eines Nukleons (hier das Proton) sprechen, anstatt ein neues Teilchen einzuführen.
Der Unterschied in der Interpretation der |
beiden angeregten Zustände wird vor allem durch
die
extrem unterschiedlichen Größenordnungen der Energien bzw. Massen verursacht. Ein Vergleich der Ruhemassen der jeweiligen Grundzustände und angeregten Zustände
macht den Unterschied deutlich:
 Die
Differenz der Massen von Proton und D
13
(1520)
beträgt
Die
Differenz der Massen von Proton und D
13
(1520)
beträgt
(1520 - 938) MeV/c
2
=
582 MeV/c
2
.
Das entspricht einem
relativen Massenzuwachs
von 582/938
=
62 %
.
Der Massenzuwachs liegt in der gleichen Größenordnung wie die Ruhemasse!
|
|
|
Die Differenz von Grundzustand und angeregtem Zustand des Quecksilberatoms beträgt im Vergleich dazu "lächerliche"
4,85 eV/c
2
. Um den relativen Massenzuwachs des Quecksilberatoms berechnen zu können, schätzen wir seine Ruhemasse ab. Das Quecksilberatom besteht aus 120 Neutronen und 80 Protonen (die 80 Elektronen rechnen wir mal nicht mit, weil sie wesentlich leichter sind). Die Ruhemasse beträgt - Protonen
und Neutronen sind in etwa gleich
|
schwer: 200
. 938
MeV/c
2
»
188 GeV/c
2
Das "
»
"-Zeichen muss hier stehen, weil die Bindungsenergie im Atomkern diesen Wert noch
etwas verändert.
 Der
relative Massenzuwachs
beträgt folglich:
Der
relative Massenzuwachs
beträgt folglich:
4,85/188
.
10
9
=
0,000 000 002 6 %
Der Massenzuwachs ist gegenüber der Ruhemasse vernachlässigbar klein.
|
|
 Zusammenfassend kann man sagen, dass, wenn der Energiezuwachs durch Anregung klein im Verhältnis zur Ruhemasse bzw. Ruheenergie des Grundzustands ist, man immer noch vom gleichen "Teilchen" spricht, das sich nur in einem angeregten Zustand befindet.
Dies ist z.B. bei
Atomen, wie dem Quecksilberatom,
und schweren
Zusammenfassend kann man sagen, dass, wenn der Energiezuwachs durch Anregung klein im Verhältnis zur Ruhemasse bzw. Ruheenergie des Grundzustands ist, man immer noch vom gleichen "Teilchen" spricht, das sich nur in einem angeregten Zustand befindet.
Dies ist z.B. bei
Atomen, wie dem Quecksilberatom,
und schweren
|
Atomkernen
der Fall.
Liegt hingegen der Energiegewinn in der Größenordnung der Ruhemasse bzw. Ruheenergie des ursprünglichen Teilchens, so interpretiert man den angeregten
Zustand als neues Teilchen. Dies ist z.B. im Bereich einzelner
Hadronen,
wie den Protonen,
der Fall.
|
|
(siehe
dazu
![zum Literaturverzeichnis; [POV 1994, S. 187 ff]](../button_gifs/booksm.gif) )
)
|