|
Wir
betrachten die
Zweikörper- streuung im Schwerpunktsystem. Zwei Teilchen A und B werden aneinander gestreut und dabei C und D erzeugt. Wieder soll uns nur das Ergebnis der längeren Rechnung interessieren, mir der aus Fermis "zweiter goldener Regel" der |
differentielle Wirkungsquerschnitt für die Zweikörperstreuung berechnet wird. Sie
lautet:
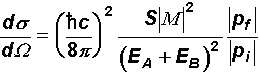
|
|