Feynman-Diagramme
und Feynman-Kalkül -
Kombinationen innerer
Linien
 Wenn
die
inneren
Linien
virtuellen Teilchen entsprechen, kann man doch
beliebige innere Linienkombinationen aufstellen?
Wenn
die
inneren
Linien
virtuellen Teilchen entsprechen, kann man doch
beliebige innere Linienkombinationen aufstellen?
Gibt es dann nicht
unendlich viele verschiedene Feynman-Diagramme zu einer Kombination
bekannter äußerer Linien?
|
Die Antwort lautet grundsätzlich "
Ja ". In der Praxis werden zuerst die äußeren Linien gezeichnet. Dann beginnt man mit der kleinsten Anzahl von Vertices, mit 2 Stück, und zeichnet alle möglichen Kombinationen innerer Linien. Dann alle Kombinationen mit 4 Vertices, 6...
usw. Man erkennt, wie schnell dabei die Anzahl der Feynman-Diagramme ansteigt.
|
|
Beispiel
:
e
-
-e
-
-Bremsstrahlung
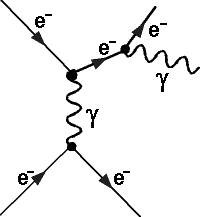
Die Elektron-Elektron-Bremsstrahlung ist ein Beispiel für einen Prozess, dessen Feynman-Diagramm eine ungerade Anzahl von Vertices besitzt. Ein anfliegendes Elektron tauscht mit einem Elektron einer Atomhülle ein Photon aus und strahlt danach noch ein einzelnes Photon ab. Die Abstrahlung
(Bremsstrahlung) des Photons führt zu einem dritten Vertex.
|
 |
|
Beispiel
:
M
Æ
ller-Streuung
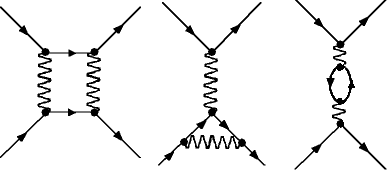
Die einfachste Möglichkeit für ein Diagramm der M
Æ
ller-Streuung ist rechts unten abgebildet (2 Vertices). Die drei rechten Diagramme (ohne Beschriftung; Pfeile sind Elektronen, Wellen Photonen) besitzen 4 Vertices und sind daher aufwendiger. Es sind bei weitem nicht alle, die man sich nur aus Elektronen und Photonen zusammengesetzt vorstellen kann.
Alle haben aber die 4 äußeren Linien, also die beobachtbaren Elektronen, gemeinsam.
Es scheint, als ob das Aufschreiben dieser Diagramme, wenn es unendlich viele davon gibt, keinen Sinn macht |
 |
Dazu
muss man Folgendes wissen:
 Alle möglichen Feynman-Diagramme eines Wechselwirkungsprozesses tragen zur Gesamtreaktion bei.
Alle möglichen Feynman-Diagramme eines Wechselwirkungsprozesses tragen zur Gesamtreaktion bei.
ABER: Je
mehr
Vertices ein Feynman-Diagramm hat, desto (deutlich)
kleiner wird
dieser Beitrag!
|
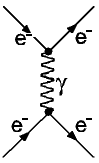 |
 Wie
berechnet man Beiträge einzelner Feynman-Diagramme?
Wie
berechnet man Beiträge einzelner Feynman-Diagramme?
Mit dem noch zu besprechenden
Feynman-Kalkül.
Wichtig ist dabei, dass zu jedem Vertex ein Faktor
 ,
die Wurzel
aus der sogenannten
Kopplungskonstanten
a
,
gehört. ,
die Wurzel
aus der sogenannten
Kopplungskonstanten
a
,
gehört.
Die
Kopplungskonstante der elektromagnetischen Wechselwirkung ist
a
= (e
2
/4
pe
0
h
c)
»
1/137
.
Die Wurzel daraus ist bis auf einen konstanten Faktor gleich der elektrischen Ladung e. Aus diesem Grund spricht man auch oft davon, dass zu jedem Vertex die entsprechende Ladung e (oder allgemein: g) gehört. Der gesuchte
Beitrag
ist proportional zum Produkt
|
aller vorkommenden
 (bzw. e oder g). Der Beitrag eines Diagramms "
zweiter Ordnung", d.h. es besitzt
2 Vertices, ist also proportional zu
e
2
~
a
,
eines vierter Ordnung (4 Vertices) ist proportional zu
e
4
~
a
2
usw. Dabei
ist:
(bzw. e oder g). Der Beitrag eines Diagramms "
zweiter Ordnung", d.h. es besitzt
2 Vertices, ist also proportional zu
e
2
~
a
,
eines vierter Ordnung (4 Vertices) ist proportional zu
e
4
~
a
2
usw. Dabei
ist:
a
»
0,0073
a
2
»
0,000053
a
3
»
0,00000039
a
4
»
0,0000000028
Man erkennt, wie stark die Beiträge der Diagramme mit steigender Zahl von Vertices, hier wurden nur die geradzahliger Ordnung angegeben, abnehmen, so dass man je nach gewünschter Genauigkeit bereits bei wenigen Vertices
abbrechen kann.
|
|
 Das Problem dabei ist allerdings, dass gleichzeitig die Anzahl der möglichen Diagramme mit wachsendem n sehr stark ansteigt. Während der Beitrag
mit
a
n
abnimmt, nimmt die Anzahl der möglichen und damit beitragliefernden
Diagramme mit n! (n! = 1
.
2
.
3
. ...
.
n)
Das Problem dabei ist allerdings, dass gleichzeitig die Anzahl der möglichen Diagramme mit wachsendem n sehr stark ansteigt. Während der Beitrag
mit
a
n
abnimmt, nimmt die Anzahl der möglichen und damit beitragliefernden
Diagramme mit n! (n! = 1
.
2
.
3
. ...
.
n)
|
zu. Da
a
n
à
0 und n!
à
¥
für n
à
¥
, kann nicht einfach entschieden werden, dass die Beiträge von Diagrammen höherer Ordnung vernachlässigbar wären. Es hat sich allerdings gezeigt,
dass die Beiträge von Diagrammen über 8. Ordnung klein sind.
|
|
Eine
große Leistung des Physikers
Kinoshita ist es, die Beiträge von Diagrammen 8. Ordnung berechnet zu haben (1981). Ausgangssituation war die Berechnung des anomalen magnetischen Moments a des Elektrons innerhalb
der QED. Experimentell war a (a
exp
)
bereits mit einer Genauigkeit von etwa 10
-10
bestimmt. Die Darstellung von a in der QED (a
QED
)
erfolgt in einer Potenzreihe mit Potenzen von
a
/
p
und
den
Entwicklungskoeffizienten C
i
:
a
QED
= C
1
(
a
/
p
)
+ C
2
(
a
/
p
)
2
+ C
3
(
a
/
p
)
3
+ C
4
(
a
/
p
)
4
...
Die
Entwicklungskoeffizienten berücksichtigen die
Beiträge der Feynman-Diagramme
2. Ordnung (C
1
),
4. Ordnung (C
2
), 6.
Ordnung (C
3
) usw..
|
Das Problem war, dass die Abweichung des QED-Werts vom experimentell bestimmten
Wert 7-mal so groß war wie die angegebenen Fehlergrenzen von a
exp.
Da bisher nur die ersten drei Entwicklungskoeffizienten C
1
,
C
2
und C
3
berechnet waren, hoffte man durch die Berechnung von C
4
die Abweichung verkleinern zu können und mit
dem neuen Wert für
a
QED
innerhalb der experimentellen Fehlergrenzen zu liegen. Zur Berechnung von
C
4
mussten insgesamt
891 Feynman-Diagramme berechnet werden. Die Arbeit hat sich gelohnt,
denn die Korrektur
C
4
(
a
/
p
)
4
war wie erhofft in Übereinstimmung mit dem Experiment. (siehe dazu
![zum Literaturverzeichnis; [KIN 1981]](../button_gifs/booksm.gif) )
)
|
|
|
Bisher
haben wir uns mit Feynman-Diagrammen auf die
Quantenelektrodynamik (QED), also nur auf
elektromagnetische Wechselwirkungen beschränkt.
Auf der
|
nächsten Seite werden wir sehen, wie Feynman-Diagramme in
der
Quantenchromodynamik (QCD), also bei der
starken Wechselwirkung
aussehen.
|
|
|